1. レンズの結像と光路図
1.1. 無限遠からの光の集光
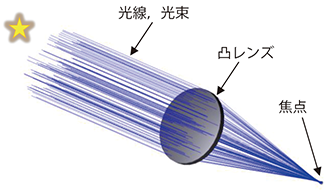
ここでは先ず、星からの光など無限遠からの光束が一枚の凸レンズで集光される場合について説明いたします。
この様子を図1に示しましたが、ここでは光が左上から右下に向かい伝播してくるとします。青色で示される線は光線（ ray of light ）を意味し、これが纏まった（束ねられた）ものを光束（ pencil of rays ）といいます。この光線・光束は無限遠の物体から到達したものですので平行光になっています。凸レンズを通った光線はレンズ表面で屈折し、焦点として集光します。
この様子を光路図として示したものが図2です。
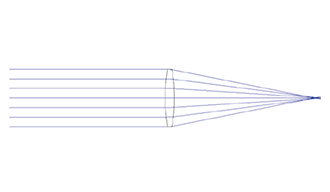
一般に光学では、光は左から右に伝播することになっていますので凸レンズの左側が物体側です。
この状況では無限遠からの光束がレンズに対し垂直に入って来ているので、中央の線が光軸に相当します。ここでは仮に光束を7本の光線で示しました。中央の光線は光軸に沿ってそのままレンズを透過しますが、それより外側の光線はレンズの各面にて屈折しながら透過し、焦点に集光しています。
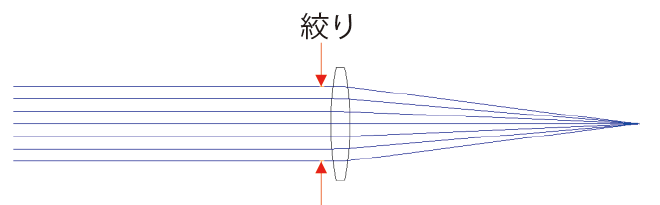
なおこのレンズが取り込める光線の量は、最大でもレンズの大きさまでとなります。したがって、この場合はレンズの外径そのものが“絞り”となります。
ここで図3に示すように凸レンズの直前に、レンズ径より小さい絞りを設けてみます。この場合、レンズの焦点距離は変わらず、物体側から見た絞りの径、即ち“入射瞳径”が小さくなったため小絞りとなり“Fナンバー”が大きくなります。このＦナンバーは、焦点に集光する光束の円錐頂角を示しているとも云えます。
これまでは光軸上の平行光束について扱ってきましたが、カメラでは像を得るためにある大きさをもつ撮像面を焦点位置に置きます。
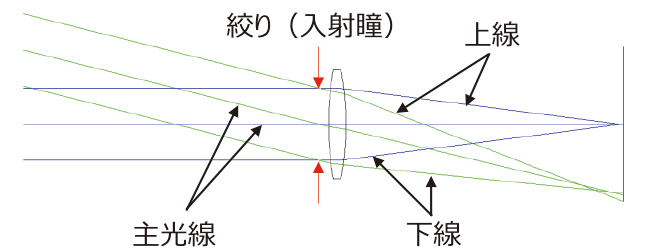
一例として、イメージサイズが対角8mm（1/2型）の撮像センサを使用し、焦点距離がf=16mm ＦナンバーがF4のレンズを用いた時の光路図を図4に示します。像高4mmに相当する画面最周辺へは、左上より右下へ向かう軸外からの平行光束がレンズに入射することが判ります。なお図4では光束を3本の光線で示しています。この3本の光線は次のように決められています。
- 主光線：絞り（入射瞳）の中心を通る光線
- 上線、上光線：入射瞳の上の縁を通る光線
- 下線、下光線：入射瞳の下の縁を通る光線
この上線と下線に挟まれた領域が結像に寄与することになります。
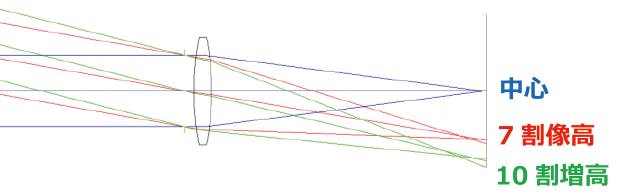
なお一般には図5に示すように、光軸上（画面中心）、及び画面最周辺（10割像高）のほか、7割像高の光線を示すことが多いです。（1/2型ですと、表示する像高は0mm,2.8mm,4mmの3箇所です。）
1.2. 有限距離物体の結像
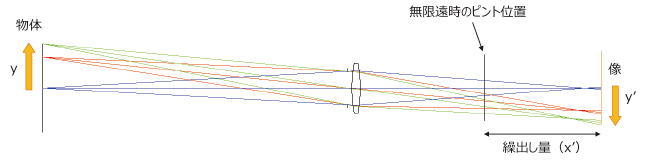
これまでは物体が無限遠にある場合を示してきましたが、ここでは物体が有限距離にある場合について説明します。物体が有限距離にある場合の結像位置は、𝑥∙𝑥′=−𝑓2 で示されるニュートンの公式により、無限遠時のピント位置に対して“繰出し量（ 𝑥′ ）”だけ離れた位置に像を結びます。
一般的なカメラは、無限遠の被写体を撮影できるように像側焦点位置に撮像センサの撮像面を配置します。この状態で有限距離の被写体を撮影すると“繰出し量”だけ像が離れるためピントがぼけてしまいますが、この量だけレンズを前に出す（繰出す）ことでピントを合わせることができるため“繰出し量”と呼びます。ピント調整が可能な撮影レンズでは、フォーカスリング（距離環）を動かすことによりこの繰出し量分だけ像の位置を動かし、撮像面と合致させることができます。またレンズのピント調整範囲外の場合やピント調整ができないレンズでは、繰出し量に相当する厚さ・長さの”接写リング“をレンズとカメラの間に挿入することでピントを合わせることができます。
また物体の大きさ（y）と像の大きさ（y′）の比が光学倍率（M）となり 𝑀=𝑦′/𝑦で示されます。
なお図6では物体と像との向きが逆さまになっているので（倒立像）、光学倍率は負（マイナス）となります。
2. 光路図におけるレンズの主要点
2.1. 像側主点の位置
“主点”とは“レンズの中心と見做せる点”を意味し、仮に“ごく薄い厚さの凸レンズ”（“薄肉レンズ”という）があるとした場合はそのレンズの位置になります。実際の撮影レンズでは一枚レンズのものでも少なからず厚みを持ち、レンズの中心位置を決めることができないため、無限遠からの平行光束を入射させ、あたかも薄肉レンズがあるように作用する点を主点とします。一般のレンズでは、光を通過できる方向が前後の二方向あるため、主点は二箇所存在します。撮影レンズの物体側から平行光を入れた場合の主点を“像側主点”、または“第二主点”、像側から平行光を入れた場合の主点を“物体側主点”、または“第一主点”といい、この二つの主点の間隔を“主点間隔”といいます。
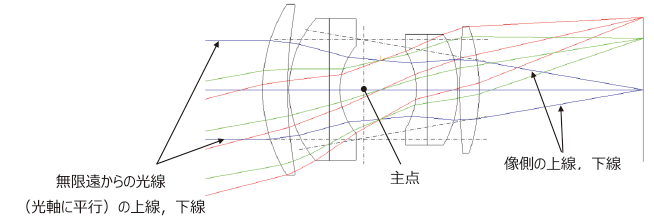
2.2. 射出瞳の位置とその重要性
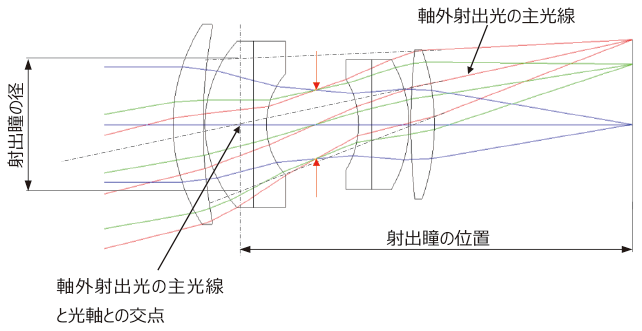
“絞り”より後ろ側にあるレンズによって作られる像（虚像）のことを射出瞳といいます。物体の一点より“絞り”を通過した光線は、“射出瞳”を底とした円錐状の光束となって結像します。したがって“射出瞳”はレンズから像面に至る光線束を決定する役目があります。
近年の撮像センサには感度向上のため各画素前に“オンチップレンズ”を配置しています。このレンズにより各画素が取り込むことのできる光の角度が決まりますが（センサの斜入光感度特性）、射出瞳位置の短い撮影レンズでは画面周辺部での光の入射角度が大きすぎて光を取り込めず、周辺光量が低下する原因になることがありますので、これを避けるには射出瞳位置の長いレンズの使用が有利です。光路図における射出瞳の位置と径を図8に示します。
3. テレセントリックレンズの光路図
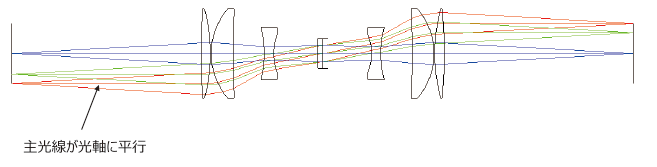
3.1. テレセントリックレンズ
レンズの主光線が光軸と平行になっている状態を“テレセントリック”と云います。
また入射瞳の位置が無限遠にあるレンズを物体側テレセントリックレンズと云い、“画角が0°”という特殊なレンズで、“被写体との距離が変化しても光学倍率が変わらない”という計測用途に適した特性を持っています。なお“画角が0°”ですから一般の撮影レンズのように撮影距離で光学倍率を変えることはできません。また原理上、被写体の大きさ以上のレンズ有効径が必要ですので、広い範囲を写すなど光学倍率が小さい場合はレンズの鏡筒や前玉が必然的に大きくなります。
両側テレセントリックレンズは、物体側、像側共にテレセントリックになっているレンズです。
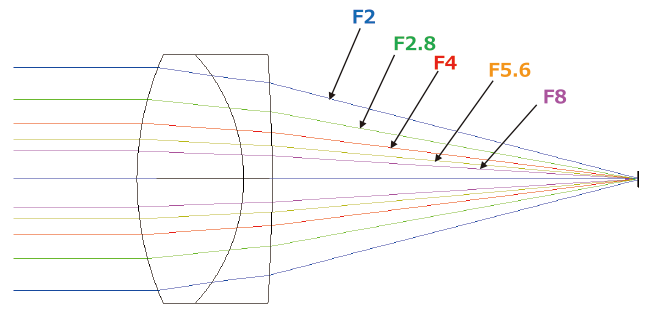
4. Fナンバーと光路図
4.1. 各Fナンバーにおける焦点に集光する光束の様子
F2からF8までのＦナンバーにおける像側の光路を図10に示しました。各Ｆナンバーによる焦点に集光する光束の円錐頂角の違いがお判かりかと思います。この頂角、あるいは円錐が光量を示すことになります。例えばF2に対してF2.8では、円錐の体積が1/2になっていますので、光量も1/2となります。
なお、Ｆナンバーは焦点距離と絞り径の比で表されますので、どのようなレンズを使用しても基本的には同じ頂角となります。
