技術情報
知っておきたい撮影レンズの倍率について
該当製品
-
CoaXPress 2.0 カメラ

-
USB3 カメラ

-
GigE カメラ

はじめに
マシンビジョンにおいては,撮影レンズの選定や光学系の検討をする際に“光学倍率”が重要になります。
しかしながら“倍率”には,物と像の大きさの比を示す一般的な結像倍率以外の意味もあることはあまり知られておらず,しばしば混同されて使用されているようです。
ここでは撮影レンズを使う立場での“倍率”の考えかたや応用について解りやすく説明いたします。
1. 光学倍率
1.1. 撮影レンズでの光学倍率
光学系による長さの変化の比を“倍率”といいます。
写真やマシンビジョンで使用される撮影レンズは“結像光学系”であり,これにおける“倍率m”には,一般的に使用されている物体と像の大きさの比を示す“横倍率β”と,それと直交する光軸方向の“縦倍率α”とがあります(これらについては次項で説明いたします)。
大きさを示す倍率の場合,同じ大きさに撮影するときは“等倍”,あるいは“1倍”といいます。また拡大する場合は“2倍”など1以上の値を,縮小する場合は“0.5倍”など1未満の値となります。
なお通常の撮影では“倒立像”となるため,倍率(横倍率β)の符号は負(-:マイナス)となりますが,一般的には負号が省略されて用いられることも多いです。
1.2. 望遠鏡や双眼鏡の倍率
結像光学系である撮影用レンズでは実像を撮影するため,物体と像との大きさを直接測定すればそれらの大きさの比である“横倍率β”を測定することが出来ます。これに対し望遠鏡や双眼鏡では,対物レンズにより作られた実像を接眼レンズを通した虚像として見ており,光軸に平行に入射した光線が光軸に平行に出射するような特殊な光学系となっています。この光学系は“アフォーカル系”や“無焦点光学系”と呼ばれ,倍率mとしては物体からの光線と光軸の傾角uと,像への光線と光軸との傾角u’との比である“角倍率γ”が用いられます1。
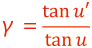
これは“1/γの距離”まで近づいた時と同じ大きさに見えることを意味しています。
倍率が大きくなると,見える範囲が狭くなったり,“瞳径”が小さくなるため像が暗くなったりするとともに構造的に大きくなります。双眼鏡の仕様としては,バードウォッチングでは携帯性が重視されるため,倍率が6~8倍で口径が30~42mmのもの2が,スターウォッチングでは7~18倍で口径が50~70mm程度のものが主に使用されています。なお高倍率の場合は,手振れを防ぐために三脚に固定して使用しますが,近年,観劇やコンサート会場では,手振れ補正付の10倍程度の防振型に人気が出てきているようです。
また瞳径は“口径÷倍率”で求められ,眼の瞳孔より小さいと見えづらくなります。このため日中に使用するものでは約3mm以上,夜間や暗い場所で使用するものでは約5mm以上の瞳径の双眼鏡が用いられます。普及形のものとしては,小形で高倍率の双眼鏡も販売されていますが,瞳径が小さくなるため,視野が暗くなったり,眼を動かすと視界が見えなく(ブラックアウト)なったりしやすいので,利用には注意が必要です。
1.3. ルーペの倍率
ルーペも虚像を観察する光学系ですが,倍率mは“明視距離の250mm”とルーペの“焦点距離f”との比で求められます。
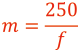
“明視距離”とは,近いものを見るときに眼の緊張が少なく,あまり疲労せずに良く見える距離のことを云い,古来より250mm(=4ディオプトリ)とされています。“本を読むときに25~30cm離しましょう”と云われるのも明視距離からきています。なお年齢が進むとともに目の水晶体の弾性が失われることで調節力が減退し,物を明視距離より遠ざけねば良く見えない状態を老視(老眼)といいます。
1.4. ズームレンズの倍率
デジタルカメラやビデオカメラで使用されるズームレンズでは,仕様として3倍や6倍,30倍などの倍率が示されますが,これは“ズーム比”と呼ばれるものであり,焦点距離の長い側の端(テレ端)と短い側の端(ワイド端)とでの焦点距離の比を示します。たとえば焦点距離が8~80mmに可変できるズームレンズではズーム比が10倍となります。
2. 縦倍率と横倍率
2.1. 横倍率
一般に光学倍率とは“横倍率β”のことをいいます。
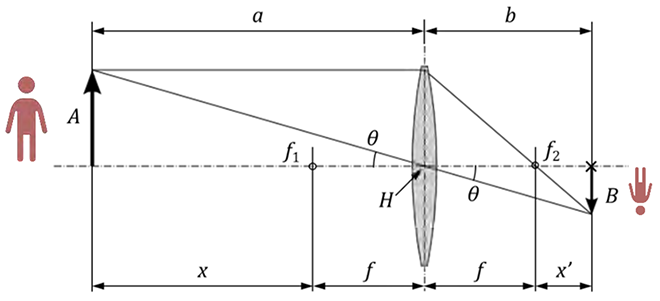
横倍率βは,物体の高さAに対する像の高さBの比です。
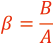
撮影距離xと繰出し量x’との関係は次式で示されます。
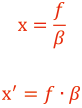
2.2. 縦倍率
“縦倍率α”は,光軸に沿った物体の微小移動量⊿xに対する像の移動量⊿x’の比です。
言い換えればピントずれの感度を示しています。
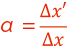
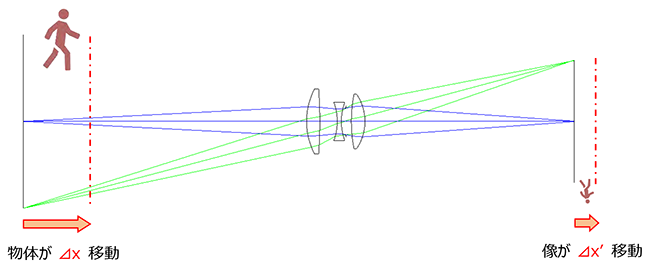
“縦倍率α“はニュートンの式を微分することで求められます。
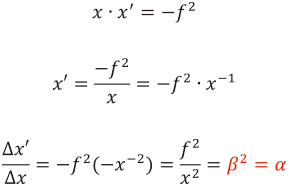
よって,物体の移動量が比較的小さい場合の縦倍率αは横倍率βの二乗となります。
3. 焦点深度と被写界深度
3.1. 被写界深度の公式
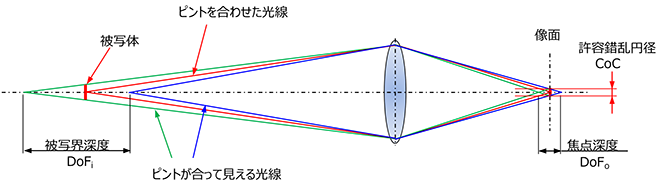
マシンビジョンで使用する一般的な撮影距離の場合,“被写界深度 DoFi(Depth of Field)”は撮像センサ側の“焦点深度DoFo(Depth of Focus)”をレンズを通して被写体側に移したものですので,上記の縦倍率αを用れば簡単に公式が求められます。
“焦点深度 DoFi”は“許容錯乱円径 CoC”,及び“有効F値 Feff”により求めます。
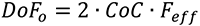
“有効F値 Feff”は撮影距離が無限遠か有限距離かで,下式により求めます。

“許容錯乱円径 CoC”は“画素ピッチ Ppix”か“エアリーディスク径 Dairy”の大きいほうとします。
“被写界深度 DoFi”は“焦点深度 DoFo”を“縦倍率 α“で割ることで求められます。
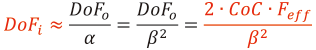
この式によると,Fナンバーが小さい(明るい)レンズ,画素ピッチの小さいセンサ,及び光学倍率が大きい(拡大)ほど被写界深度の幅は狭くなります。
なお上記式で求めた被写界深度DoFiはマシンビジョン用途など撮影距離が短い場合に使用出来ますが,監視用途など撮影距離が長い場合は,被写体に対し手前側と奥側とで大きく深度が異なります。
この場合は “焦点深度 DoFo”と“ニュートンの結像公式”を使って“被写界深度 DoF3”を求めます3。