Technology

Which lens should I use to capture this image

PDF

Applicable products

CoaXPress 2.0 Camera
- EX Series
USB3 Camera
- DDU series / DU series
- BU series
GigE Camera
- BG series
Camera Link Camera
- BC series
- CSC series

Introduction

Machine vision requires a photographic lens to project an image of an object onto a camera’s image sensor.

Its selection method is described in our product brochures and on our website as well as in commercially available books and trade journals.

However, we receive many questions about the relationship between a field of view (FoV, i.e., the area of the inspection captured on the camera’s image sensor) and a camera’s optical system although it can be calculated very easily.

This white paper gives several examples to plainly describe how to select a camera lens that satisfies your FoV requirement.

1. Field of view and camera’s optical system

First, let us discuss the field of view and a camera’s optical system, which are the basics in selecting a camera lens.

1.1. What is the field of view? What is the difference between the field of view and the angle of view?

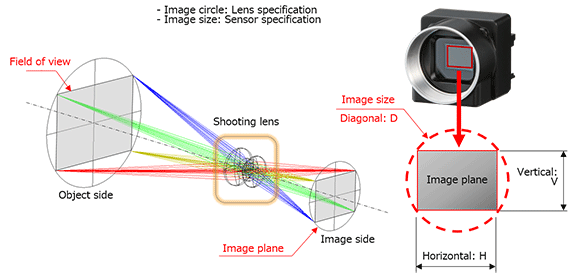
The field of view (FoV) is the extent of a physical scene that is captured by a camera’s optical system. Suppose, for example, that the whole area of A4-size paper fills the entire screen. Then, the A4 size is the field of view.

The role of a camera lens is to focus an image of an object onto an image sensor.

A flux of light that is transmitted from a lens and travels to the sensor plane forms a cone shape. The cross-section of this cone is called an image circle. The image of an object can be captured when the image circle is adequately projected onto the sensor plane. Typically, a sensor is rectangular or square. Therefore, an image projected by a lens is cut off in the shape of a rectangle of a certain size (called the image size). Since the aspect ratio of a sensor (i.e., the ratio of the width to the height of a sensor) is not fixed, the field of view depends on a camera’s sensor. Specifically, it can be calculated from the lens equation.

Figure 1 illustrates an image circle, a sensor’s image size, and a field of view.

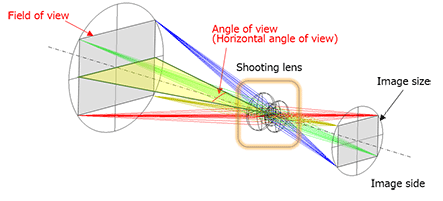
Figure 1. Image circle, image size, and field of view

The angle of view (AoV) is similar to but different from the field of view. The field of view is represented as an extent of a physical scene captured by a camera whereas the angle of view is represented as an angular extent of an image captured by a camera. The object size is not determined by the angle of view alone. Since machine vision is used to capture a specific object located at a finite distance, it is more convenient to use the field of view. The angle of view is used for photography scenarios requiring an infinity or undefined focus distance such as landscape photography. However, the term “angle of view” is customarily used interchangeably with the term “field of view” (for example, in TV programs). It is therefore necessary to discern which is meant based on context.

Half the angle of view is used especially for optical calculation.

Figure 2 illustrates the field of view and the angle of view.

Figure 2. Field of view versus angle of view

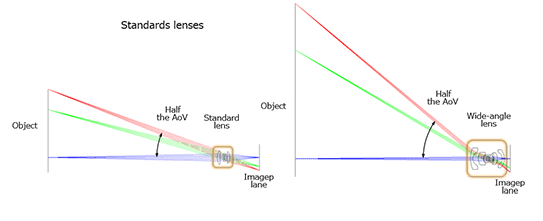
Various types of lenses are available for typical interchangeable-lens cameras (ILCs) such as standard and wide-angle lenses.

There are various definitions of “standard lens” such as a lens that reproduces a field of view close to the naked eye, but it would be correct to say that a standard lens is a lens with a focal length about equal to the diagonal size of a sensor.

For example, in the case of a camera with an image size of 1/2-inches (an 8-mm diagonal), lenses with a focal length of about 8 mm are regarded as standard lenses. In the case of a 2/3-inch camera (with a 11-mm diagonal), lenses with a focal length of about 11 mm are regarded as standard lenses. These lenses provide an angle of view of about 53°. Generally, lenses with angle of view of 45° to 60° are called standard lenses.

A lens that lets you take photographs with a wider view (i.e., a lens with a wider-angle view) than the standard lens is called a wide-angle lens. A wide-angle lens is used for machine vision applications that need to capture a wide area at a close distance. Lenses with a shorter focal length (i.e., short-focus lenses) provide a wider angle of view.

Figure 3 illustrates standard and wide-angle lenses.

Figure 3. Standard lens versus wide-angle lens

1.2. Lens equation

Figure 4 shows a geometric relationship between an object and its image formed by an optical lens. It is simplified for the sake of clarity.

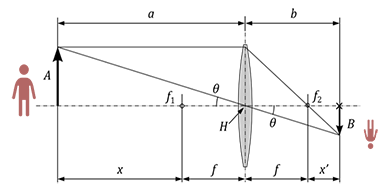
A : Height of an object from the optical axis
B : Height of an image from the optical axis (called image height)
a : Distance from the center of a lens (principal point H) to an object
b : Distance from the center of a lens (principal point H) to an image
x : Distance from the front focal point (f 1) to an object (object distance)
x’ : Distance from the rear focal point (f 2) to an image (generally called lens extension)
f : Focal length
f¹ : Front focal point
f² : Rear focal point
θ : Half the angle of view (angle of view = 2×θ )

The focal length (f) is a constant that represents one of the major characteristics of a lens. You need to calculate the focal length to select an appropriate lens according to your shooting requirements.

Newton’s lens formula represents the relationship among the focal length (f), object distance (x), and lens extension (x’):

x∙x^' = f^2

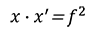
With machine vision, the object size (i.e., the field of view) is predetermined. It is therefore convenient to use optical magnification that is determined by the field of view and the sensor size when selecting a lens.でThere are transverse (also called lateral or linear) magnification (β) and longitudinal magnification (α). Here, transverse magnification is used.

Transverse magnification (β) refers to the ratio of image height (B) to object height (A):

β=B/A

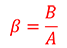
The following equation represents the relationship between the object distance (x)and the lens extension (x’):

x=f/β

x^'=f∙β

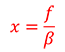
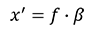
This equation can be rewritten as follows to calculate the focal length (f) of a lens from the field of view (A), sensor size (B), and object distance (x):

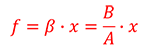
f=β∙x=B/A∙x

2. Lens selection examples

2.1. Questions

Here, we will explain in detail how to select a shooting lens. To make it easier to understand, we have prepared the following three examples.

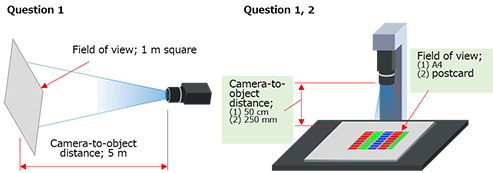
Question 1: Shooting an object 1 m square from a distance of 5 m
Question 2: Shooting an A4-size object from a distance of 50 cm
Question 3: Shooting a postcard (about the A6 size) from a distance of 250 mm

Question 1, 2, 3

2.2 Camera sensor size

To select a lens, you need to choose which camera to use first.
Here, let us assume that you will be using the BU040M, Teli’s small CMOS USB3 camera.
Table 1 shows the optical specifications of the BU040M.

Camera model	Sensor model	Image size		Resolution		Sensor size（mm）
Camera model	Sensor model	type	mm	H	V	H	V
BU040M	IMX287LLR	1/2.9	6.2	720	540	4.968	3.726

Table 1. Optical specifications of Teli’s BU040M USB3 camera

Of the camera specifications, pay attention to the sensor size to choose a lens.

The image size is expressed as the diagonal size of a sensor. Although Table 1 shows the diagonal size in mm, it is also often given in inches (“). If you choose a lens with an image circle larger than the image size of the sensor, the periphery of the image is not cut off. To select an appropriate lens according to the field of view, you need to know the sensor size.

Although the sensor size should be shown in product brochures or specifications because of its need, it is not often listed perhaps because of a lack of space. If so, calculate the sensor size by multiplying the pixel pitch (or the pixel size) of the sensor by the horizontal or vertical resolution. For example, Table 1 does not show the pixel pitch of the BU040M. However, since it has a pixel pitch of 0.0069 mm and a vertical resolution of 540 pixels, its height can be calculated as follows Sensor height = 0.0069×540 = 3.726 mm

2.3 Calculating the field of view and the optical magnification

1. Questions

Let us see the questions shown in Section 3.1 again:

Question 1: Shooting an object 1 m square from a distance of 5 m
Question 2: Shooting an A4-size object from a distance of 50 cm
Question 3: Shooting a postcard (about the A6 size) from a distance of 250 mm

2. Camera’s orientation

Generally, the height (vertical resolution) of a sensor is smaller than its width (horizontal resolution). It is therefore practical to make a calculation using the sensor height so that the field of view will not be cut off. Here, let us suppose that the camera is positioned horizontally to shoot A4- and A6-size objects in portrait orientation so that their full height fits in the height of the sensor.

3. Field of view and optical magnification (transverse magnification)

Calculate the optical magnification (transverse magnification, β) from the field of view (height of the object) and the height of the sensor. The fields of view of the objects are as follows:

Question 1: The field of view is 1,000 mm since the object is 1 m square.
Question 2: The field of view is 297 mm since the A4-size object is shot in portrait orientation.
Question 3: The field of view is 148 mm (which is equal to the height of the A6 size) since the postcard is shot in portrait orientation.

Look at Figure 4. In this figure, half the field of view is equal to the object height (A), and the half the image height is B. Here, the height of the object is 2A, and the height of the sensor is 2B.

Therefore, in the case of Question 1, the transverse magnification (β) can be calculated as follows:

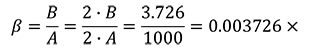
β=B/A=(2∙B)/(2∙A)=3.726/1000=0.003726×

where “x” indicates the optical magnification.

For Question 2 and Question 3, the transverse magnification (β) can be obtained in the same manner. Table 2 shows the calculation results.

4. Camera-to-object distances

The camera-to-object distances are as follows. Generally, the unit of measure used for the camera-to-object distance is mm.

Question 1: 5 m = 5,000 mm
Question 2: 50 cm = 500 mm
Question 3: 250 mm

Figure 4 shows two distances, a and x. a is the distance from the center of the lens (principal point, H) to the object whereas x is the distance from the front focal point (f 1) to the object. Since we have not calculated the focal length of the lens yet, let us assume x=a.
Hence, in the case of Question 1, the camera-to-object distance (x) is: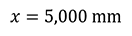 x=5,000 mm Calculate the camera-to-object distance for Question 2 and Question 3 in the same manner. Table 2 shows the calculation results.

5. V. Calculating the focal length and the image size to select lenses

At Steps III and IV, the transverse magnification (β) and the camera-to-object distance (x) were obtained. So, it is now easy to calculate the focal length of the lens.

In the case of Question 1, the focal length (f) is calculated as follows: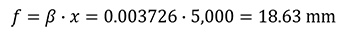 f=β∙x=0.003726∙5,000=18.63 mm Therefore, a lens with a focal length of 18.63 mm meets the requirement set forth in the question. However, the focal length of commercially available machine vision lenses (such as C-mount lenses) is limited. So, select a lens with a focal length equal to or slightly smaller than the calculation result from the product series that meets the image size of the camera.

Since the BU040M has a 1/2.9-inch image size (6.2-mm diagonal), you can use any lenses with the same mount and an image circle larger than 1/2 inches. (With 1/3-inch lenses, the periphery of an image might be cut off.)

When you look for C-mount lenses with a focal length smaller than the calculation result (18.63 mm), you will find that lenses with a focal length of 16 mm are available from lens manufacturers, from which you can select one.

Table 2 shows the calculation results for each question. Table 3 shows the focal lengths of typical C-mount lenses.

Question		Question 1	Question 2	Question 3
Object size		1m square	A4	Postcard
Vertical FoV (mm)	2*A	1,000	297	148
Transverse magnification (×)	β	0.003726	0.012545	0.025176
Camera-to-object distance (mm)	x	5,000	500	250
Focal length (mm)	f	18.63	6.27	6.29
Lens selected (mm)	f	16	6	6

Table 2. Calculation results

Focal length (mm)	f	6	8	12	16	25	35	50	75
FoV / AoV Optical transverse magnification		Lower magnification Wider FoV Higher magnification Narrower FoV

Table 3 Focal lengths of typical C-mount lenses

This white paper has described the procedure for selecting a lens suitable for a given field of view. You can follow this procedure to select the optimum lens for your application.

Here, we have discussed how to select a lens based on the focal length. Other lens specifications include the f number indicating the aperture opening. Also pay attention to the f number when selecting a lens.